It's not surface energy

Only good for geckos

If a human could place two pads, each 10cmx10cm, onto their hands and in perfect contact with a surface such as a flat vertical sheet of glass, the adhesion forces are so large that climbing up the glass would not be a problem - each pad would have enough adhesive force to support the person's weight. So the forces from surface energy are impressive. All that weight is being supported by Van der Waals forces which are powerful over a fraction of a nm. That's how geckos manage to walk up walls.

However, the gecko (and the human) have to move and strong adhesion would be useless. The point about surface-energy adhesion is that the slightest crack at the interface (caused by flexing the gecko's foot or the human's hand) breaks the adhesion very easily.

The video shows this principle perfectly. My neighbours, Tony and Anna Chester kindly gave me permission to use this video showing the difference between gecko strength against a pure pull (we really were pulling as hard as we could) and the weakness of the bond against a "real" adhesion test when pulled along the line of the bond. Those are just two pieces of very smooth rubber. The hard part of the experiment was attaching the handles to the back of the rubber using the strongest possible tape.

In other words, surface energy adhesion is useless when we really want two surfaces to stay together and resist the harsh forces that tend to pull them apart. See the Red Herring video described under Resources for another myth around surface energy and adhesion.

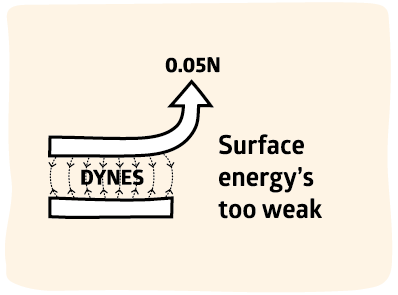
2500x too small

In fact, we know that surface energy must be irrelevant for strong adhesion. Good adhesion is typically 100N/m. Surface energy is 40dyne/cm or 0.04N/m, a factor of 2500 below what we need.

And if you could double the surface area by roughening (nearly impossible to do) you would only get 0.08N/m, a factor of 1250 too small. Why do I say that doubling the surface area is nearly impossible? If you look at a typical surface scan of a surface that has been deliberately roughened it might look like something found on my Surface Profile Explorer page:

It is rather obvious to the eye that an ant crawling along this surface would have to cover a huge distance up and down the mountain peaks and valleys compared to the equivalent journey if the surface were completely flat. So the increase in surface (and therefore of surface energy adhesion) must be huge. But this is an artefact of the Y-axis scale. The X-axis is a typical 12.5mm scan and the Y-axis goes to a maximum of 60μm

When the graph is scaled (so the Y-axis is 12500μm, i.e. 12.5mm) then the true nature of the "rough" surface is revealed. The app does the calculation for you. When the surface has 50μm peaks (that's a rough surface!) then the extra distance the ant travels up and down the "mountains" is just 5%.